Limite matemático
En matemática, el concepto de límite es
una noción topológica que formaliza la noción intuitiva de
aproximación hacia un punto concreto de una sucesión o una función,
a medida que los parámetros de esa sucesión o función se acercan a un
determinado valor.
En cálculo (especialmente en análisis real y matemático)
este concepto se utiliza para definir los conceptos fundamentales
de convergencia, continuidad, derivación, integración,
entre otros. Si bien, el concepto de límite parece intuitivamente relacionado
con el concepto de distancia, en un espacio euclídeo, es la clase de conjuntos
abiertos inducidos por dicha métrica, lo que permite definir
rigurosamente la noción de límite.
El concepto se puede generalizar a otros espacios
topológicos, como pueden ser las redes topológicas; de la misma manera, es
definido y utilizado en otras ramas de la matemática, como puede ser la teoría
de categorías.
Para fórmulas, el límite se utiliza usualmente de
forma abreviada mediante lim como en lim(an) = a o se
representa mediante la flecha (→) como en an → a.
Ahora bien , tal vez cambiando un poco de tema pero que esta relacionado con los limites son las funciones y sus graficas, a continuación verá alguna de las mas importantes y como aprender rápidamente en que dirección van para tener una idea:FUNCION LINEAL:
Para trazarla basta con hallar dos puntos y unirlos.
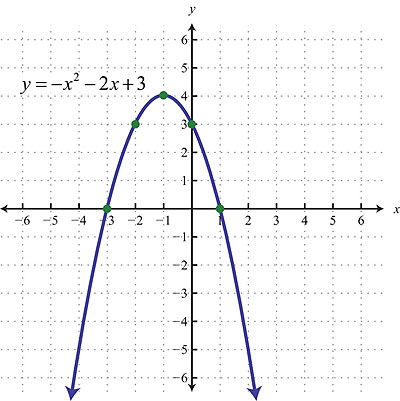
FUNCION CUADRÁTICA
Para trazarla se busca el vértice, y se le dan valores a cada lado de este.
Puede abrir hacia arriba si el primer termino en la función es positivo o hacia abajo si es negativo.
En la imagen la función abre hacia abajo.
FUNCION CÚBICA
Siempre empieza en el eje horizontal y sube hasta infinito,
nótese que en el eje X pareciera que llegara a ser cero pero nunca lo toca.
__________________________________________________________________________
Bueno, y para entrar ya a lo que es en sí el concepto de limite y mejor aun, su aplicación vamos a ver este ejercicio con una función racional:
*Función racional= Es aquella función donde tiene en la mayoría de casos un polinomio en el numerador y denominador
*Asintota=Es una linea que cuando se prolonga, se podría decir hasta infinito,se va acercando lentamente a una curva pero no la toca.
Existen 2 tipos de Asintotas=Verticales y horizontales.
*Lo primero que se debe hacer son buscar las Asintotas dentro de la función
*Las asintotas verticales son los ceros del denominador y para hallarlas se saca el denominador, se iguala a 0 y se resuelve.
En este caso al factorizar, se puede cancelar con el numerador quedando así:
Después de hallar la asintota vertical, se procede con la horizontal, pero ¿Cómo la hallamos?
-Cuando el grado del numerador es menor que el del denominador , la asintota horizontal es 0.
-Cuando el grado del numerador es mayor que el del denominador, NO hay asintota horizontal.
-Si el grado del numerador y el denominador son iguales ,la asintota horizontal es el numero que acompaña a la variable con el exponente mayor.
EN ESTE CASO LA ASINTOTA HORIZONTAL ES CERO.
Siguiente a este paso, se traza el eje X y se ubican las asintotas , se dibujan con linea intercalada, las asintotas verticales crean los intervalos, para el ejercicio sería (-(X),3) y (3, (X)) ,a partir de esto con ayuda de la calculadora se empiezan a dar valores por la izquierda y luego por la derecha, (que los valores no sean tan cercanos entre ellos)para ver hacia donde se dirigen esas curvas y poder saber si existe el limite o no.
EXISTENCIA DE UN LIMITE
Para saber si existe un limite, en un determinado punto se tiene que verificar por el lado izquierdo y lado derecho en la gráfica. Si el limite por la izquierda es diferente al limite por la derecha el limite NO EXISTE. Tienen que ir ambas curvas hacia el mismo lado
EXISTENCIA DE UN LIMITE
Para saber si existe un limite, en un determinado punto se tiene que verificar por el lado izquierdo y lado derecho en la gráfica. Si el limite por la izquierda es diferente al limite por la derecha el limite NO EXISTE. Tienen que ir ambas curvas hacia el mismo lado
En este caso ya le dimos varios valores, y el resultado fue que por la izquierda se iba yendo hacia menos infinito y por la derecha se iba yendo hacia infinito positivo por lo tanto el limite no existe cuando X = 3
**********************************LIMITES***************************************




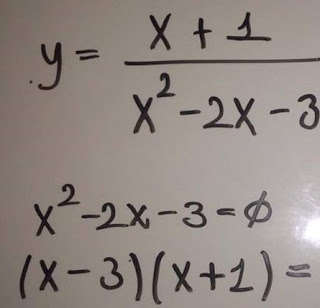




No hay comentarios:
Publicar un comentario